Análise de Questão do Enem Envolvendo Função Afim

Neste final de semana, publicamos um artigo esclarecendo o conceito e o uso da Função Afim, conteúdo da matemática que também é muito usado na disciplina de Física (veja a matéria).

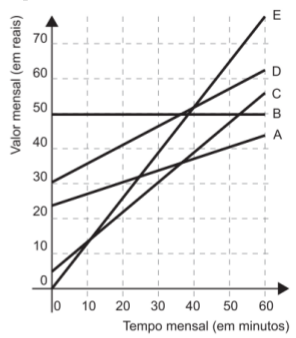
Para ilustrar e fixar o conteúdo estudado, trazemos hoje um exemplo de questão do Enem que exige o uso e o conhecimento de uma função afim.

Enem 2014 – Questão 160 – Caderno Amarelo

No Brasil há várias operadoras e planos de telefonia celular.

Uma pessoa recebeu 5 propostas (A, B, C, D e E) de planos telefônicos. O valor mensal de cada plano está em função do tempo mensal das chamadas, conforme o gráfico.

Essa pessoa pretende gastar exatamente R$ 30,00 por mês com telefone.

Dos planos telefônicos apresentados, qual é o mais vantajoso, em tempo de chamada, para o gasto previsto para essa pessoa?

a) A
d) D
b) B
e) E
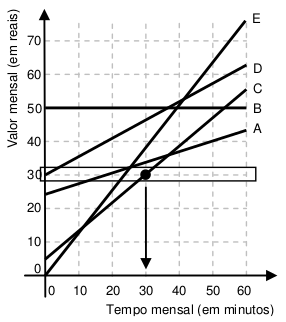
c) C

RESOLUÇÃO E COMENTÁRIOS

Alternativa C

A resolução desta questão provém totalmente da interpretação do gráfico. Nele, devemos observar a faixa onde o gasto mensal é R$ 30,00. Em outras palavras, observar a linha horizontal onde o valor no eixo y é 30. Daí, analisando esta faixa, devemos procurar qual das cinco retas cruza a linha horizontal mais à direita. Ela representará o maior tempo mensal de chamadas, em minutos, para o gasto previsto de R$ 30,00, ou seja, a proposta mais vantajosa.

Vamos ao gráfico:

Analisando cada reta, vemos que das cinco, a única que não está na faixa dos R$ 30,00 é a reta B. A reta A, para um gasto de R$ 30,00 permite 20 minutos. A reta C, 30 minutos. Já a reta D não permite nenhum minuto e a reta E um pouco mais de 20 minutos, mas menos que 30.

Logo, dos planos apresentados, o mais vantajoso em tempo de chamadas para um gasto de R$ 30,00 é o plano C.

Comentário: O único conceito necessário para resolver a questão diz respeito à localização de pontos no plano cartesiano.

Conteúdos envolvidos: Interpretação de gráficos.

Como deve ter percebido, o enunciado acaba exigindo do candidato conhecimentos e boa interpretação de uma função afim. Entretanto, utiliza uma situação do cotidiano para elaborar a questão, como faz costumeiramente.

Portanto, não tem saída. Uma preparação completa para o Enem envolve resolver diversas questões que já apareceram em edições anteriores.