Função afim e Movimento Uniforme (MU)

Todo estudante sabe (ou pelo menos deveria saber!) que existe uma relação muito íntima entre matemática e física. Tanto que, geralmente, quando não gostamos de um, automaticamente não gostaremos do outro.

Hoje, falaremos sobre a Função afim, um dos assuntos mais frequentes da matemática, e como ela pode ser utilizada no estudo do Movimento Uniforme (MU) – movimento que não apresenta variação de velocidade.

Primeiramente, vamos olhar as características da função afim.

A função afim também pode ser chamada de Função de Primeiro Grau, ou seja, a variável (geralmente nomeada “x”) estará elevada à primeira potência. Conceituando, a função afim é toda aquela função f de IR em IR dada por uma lei da forma f(x) = ax + b, onde “a” e “b” são números reais dados. O número “a” (obrigatoriamente diferente de zero) é chamado de coeficiente de x e o número b é chamado termo constante.

O gráfico de uma função afim é uma reta não perpendicular ao eixo Ox, como os representados na figura abaixo.

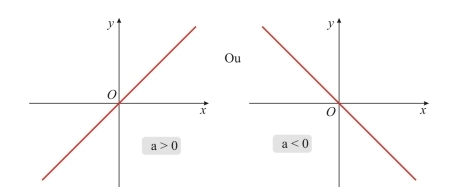
Nos gráficos acima, o termo constante é zero.

Um exemplo prático onde a função afim pode ser observada é no estudo de Movimento Uniforme (MU), conteúdo introdutória da cinemática, umas das áreas da Física.

A equação da posição, também conhecida como função horária da posição (posição em função do tempo), é geralmente vista como: S=So+v.t

Como a equação é em função do tempo, o tempo (t) é a variável (x). Logo, o coeficiente da variável (a) é a velocidade (v) e o espaço inicial (So) é a constante (b). Modificando a equação, podemos perceber mais facilmente que o movimento retilíneo uniforme é exatamente uma função afim (função de primeiro grau).

S= So+v.t
S=v.t + So (substituindo as letras)
S= a.x+b
S=f(x)
F(x)=a.x+b

Portanto, o gráfico que representa o movimento uniforme terá o tempo como eixo horizontal, o espaço como eixo vertical e sempre será uma reta. Como não há tempo negativo, toda a parte do gráfico em que x<0 desconsiderada.="" deve="" p="" ser="">